Introduce

迪菲-赫尔曼密钥交换（英语：Diffie–Hellman key exchange，缩写为D-H） 是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。公钥交换的概念最早由瑞夫·墨克（Ralph C. Merkle）提出，而这个密钥交换方法，由惠特菲尔德·迪菲（Bailey Whitfield Diffie）和马丁·赫尔曼（Martin Edward Hellman）在1976年首次发表。马丁·赫尔曼曾主张这个密钥交换方法，应被称为迪菲-赫尔曼-墨克密钥交换（英语：Diffie–Hellman–Merkle key exchange）。

虽然迪菲－赫尔曼密钥交换本身是一个匿名（无认证）的密钥交换协议，它却是很多认证协议的基础，并且被用来提供传输层安全协议的短暂模式中的完备的前向安全性。

Theory

最简单，最早提出的这个协议使用一个素数$$$p$$$的整数模$$$n$$$乘法群以及其原根$$$g$$$。下面展示这个算法，绿色表示非秘密信息, 红色表示秘密信息：

  1. 爱丽丝与鲍伯协定使用 $$\color{green}{p=23}$$以及base $$\color{green}{g=5}$$
  2. 爱丽丝选择一个秘密整数 $$\color{red}{a=6}$$ 计算 $$\color{green}{A =g^{\color{red}{a}} \bmod p}$$并发送给鲍伯。
    • $$\color{green}{A =5^{\color{red}{6}} \bmod 23 = 8}$$
  3. 鲍伯选择一个秘密整数 $$\color{red}{b=15}$$ 计算 $$\color{green}{B =g^{\color{red}{b}} \bmod p}$$并发送给爱丽丝。
    • $$\color{green}{A =5^{\color{red}{15}} \bmod 23 = 19}$$
  4. 爱丽丝计算 $$\color{green}{\color{red}{s} =B^{\color{red}{a}} \bmod p}$$
    • $$\color{green}{\color{red}{s} =19^{\color{red}{6}} \bmod 23=\color{red}{2}}$$
  5. 鲍伯计算 $$\color{green}{\color{red}{s} =A^{\color{red}{b}} \bmod p}$$
    • $$\color{green}{\color{red}{s} =8^{\color{red}{15}} \bmod 23=\color{red}{2}}$$

ECDH

ECDH 全称（Elliptic Curve Diffie–Hellman key exchange），是基于椭圆曲线的 DH 算法。

假设有私钥 $$$d$$$, 则有 $$$P=dG$$$ 为公钥。

生成一个临时私钥 $$$k \in (0, n)$$$，则得到 $$$Q=kG$$$ 为临时公钥，同时得到 $$$S=kP$$$ 为共享秘密。

根据公式 $$$S=kP=k(dG)=d(kG)=dQ$$$ 可知，通过 $$$dQ$$$ 也可以计算出一样的共享秘密。

其交互过程救命如下：

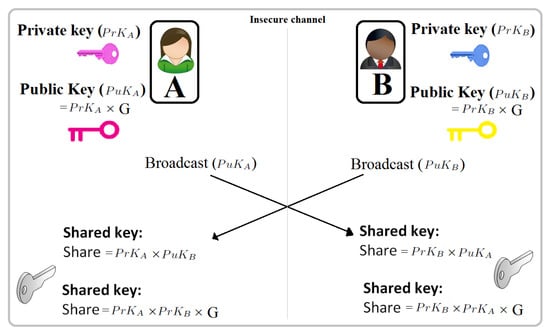
Demo

http://andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/

Reference

  1. https://zh.wikipedia.org/wiki/迪菲-赫爾曼密鑰交換
  2. https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange
  3. https://en.wikipedia.org/wiki/Elliptic_curve_Diffie%E2%80%93Hellman
  4. https://en.wikipedia.org/wiki/Curve25519
  5. https://www.cryptopp.com/wiki/Diffie-Hellman